How Do Euler Angles Work?

Written By Peter Shull

Posted on October 6, 2023 by Peter Shull

Euler angles intuitively describe orientations in 3D space

What are Euler angles and how did they originate?

Euler angles are a set of 3 sequential angles ($\alpha, \beta, \gamma$) that describe 3D orientations, and follow Euler's rotation theorem:

Euler’s rotation theorem: Any arbitrary orientation in three-dimensional space can be described with only three angles.

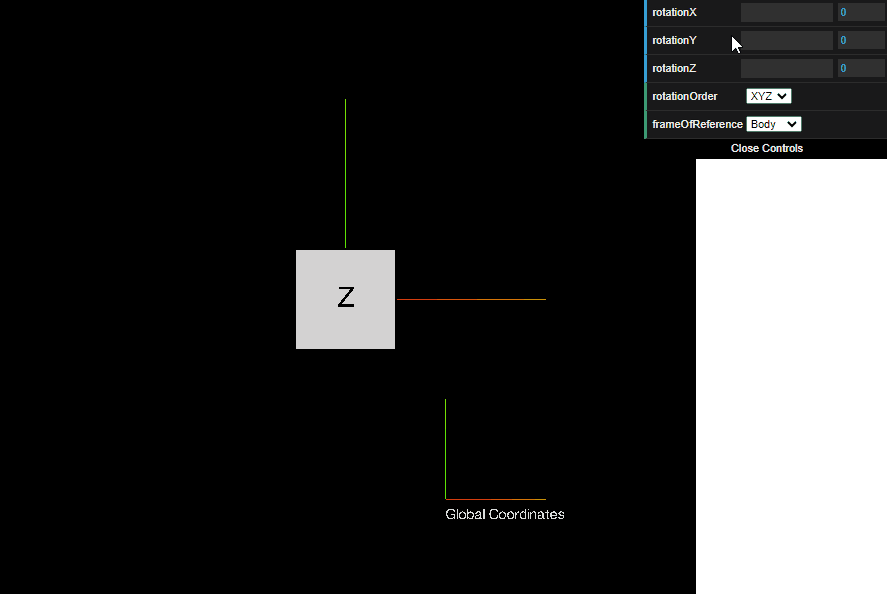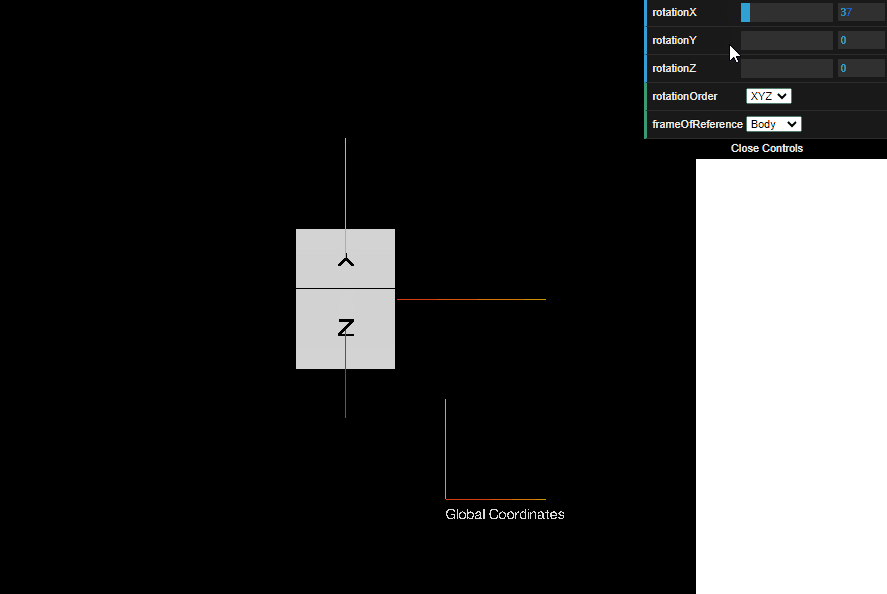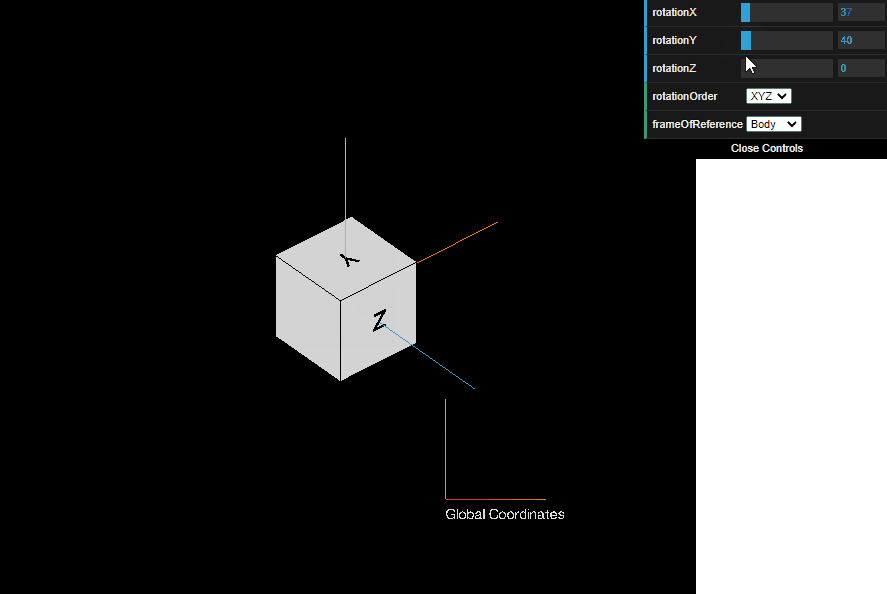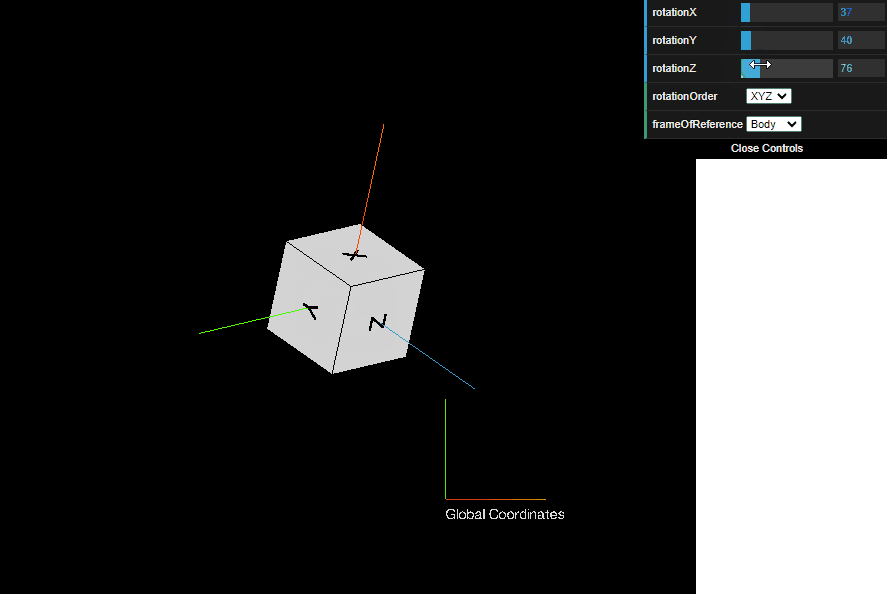
To get a feel for how Euler angles can describe any arbitrary 3D orientation, here’s an example of a sequence BodyXYZ Euler angle rotation (see below for all 24 possible Euler angle sequences). The first rotation is around the body’s X axis, the second rotation is around the body’s Y axis, and the third rotation is around the body’s Z axis.

BodyXYZ Euler angle rotation. Rotations are about body frame axes in the order: 1) x-axis, 2) y-axis, 3) z-axis.

Leonhard Euler, a Swiss mathematician, formulated Euler angles by proving Euler’s rotation theorem in 1775 using spherical geometry. He is considered one of the greatest mathematicians of all time.

Who was Leonhard Euler?

  • First to use $f(x)$ to denote functions

  • First to use $i$ to denote $\sqrt{-1}$

  • First to use $\Sigma$ to denote summations

  • First to use $\Delta$ to denote finite differences

  • First to develop rigid body equations for linear momentum, angular momentum, and motion

  • Published 384 articles while working in Germany and Russia

  • Developed the Euler Number, $e$ for the natural logarithm

  • Developed the Euler Identity, $e^{i \theta} = cos \theta + i sin \theta$ for complex numbers

  • And, developed Euler Angles, $(\alpha, \beta, \gamma)$ for 3D orientations!

But enough about Leonhard. Euler angles are essentially a series of 3 sequential rotations that define a 3D orientation. Rotations are either around axes of the body frame or the global fixed frame (sometimes referred to as intrinsic and extrinsic rotations, respectively), and the 3 rotations can be performed around either 3 different axes (called Tait-Bryan angles) or 2 different axes (called proper Euler angles).

These are all of the possible sequences of Euler angles rotated about either the body frame or the global fixed frame:

 

All 24 possible Euler angle sequences. Body denotes rotations about the body frame. Global denotes rotations about the global fixed frame. The 3 letters at the end denote the order of rotations about each named axis.

 

Now that we know what Euler angles are and where they came from….

Why are Euler angles so widely used?

Of the 4 commonly-used methods for representing 3D orientations (rotation matrices, Euler angles, angle-axis and quaternions), Euler angles are the most intuitive and the most efficient. In many technical disciplines, each rotation angle has a unique specific name, making it well suited to be described and defined with Euler angles. For example, in biomechanics, 3D knee rotation angles are commonly referred to as flexion/extension, adduction/abduction, and internal/external rotation. In aviation, the same angles are referred to as pitch, roll, and yaw.

Euler angles are an intuitive way to describe 3D orientations in various fields including for biomechanics to describe knee flexion/extension, adduction/abduction, and internal/external rotation, and in aviation to describe pitch, roll, and yaw.

Euler angles are also very efficient in that 3 numbers alone fully describe 3D orientations as compared with 4 numbers required for angle-axis and quaternions and 9 numbers required for rotation matrices. Euler angles thus generally require less computation time, which is important for many real-time applications.

Problems with Euler angles

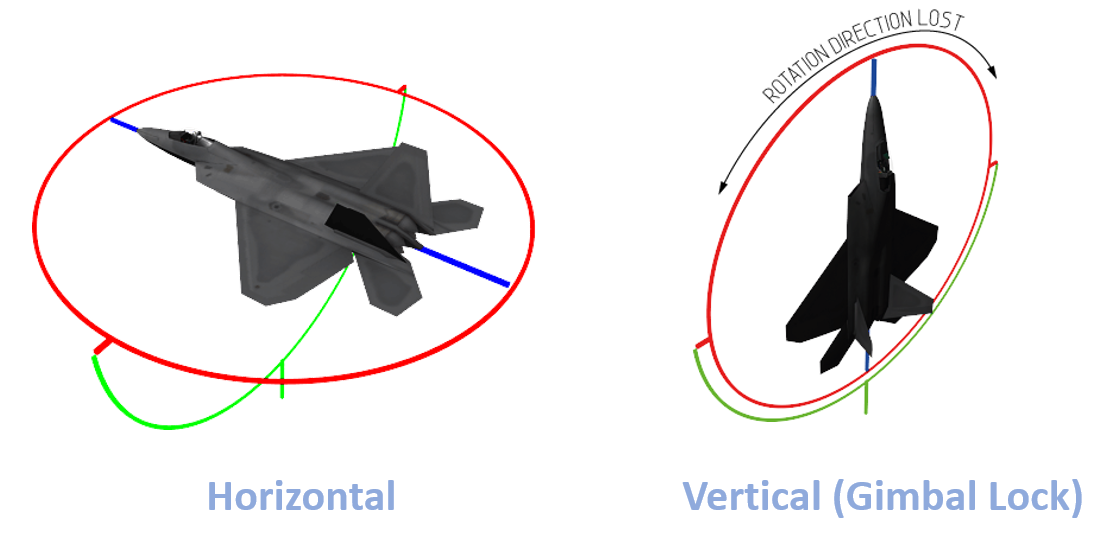
The primary problem with Euler angles is that they contain singularities at 0 or 90 degrees that lead to gimbal lock. When this occurs, 2 axes are parallel and it is not possible to rotate independently about the about a third “locked” axis. For example, if using Euler angles to describe an airplane that is rotated upward 90 degrees about it’s pitch axis so that it is pointing straight up, the yaw and roll axes become the same (green and blue axes in the figure below), and one degree of freedom is lost or “locked”. In this case, it’s not possible to independently describe tilt towards the left or right wings.

Example of gimbal lock when using Euler angles. When the airplane is vertical, the left and right rotational degree of freedom is lost or “locked” because the green and blue axes are aligned.

If the application of Euler angles doesn’t involve angles at or near the singularities, then this problem goes away (e.g. commercial airplanes don’t fly vertically, although that would be fun if they started).

The other potential problems are that successive rotations and interpolation/extrapolation can be difficult to impossible with Euler angles and if those are important it may be better to choose other 3D orientation representations (See quaternions, table “3D Orientation Representation Comparison”).

How are Euler angles calculated?

Euler angles are intuitive and are thus often measured directly from a known starting 3D orientation with domain specific terms such as knee flexion/extension, adduction/abduction, and internal/external rotation in biomechanics, and pitch, roll, and yaw in aviation as described in the “Why are Euler angles so widely used?” section above.

Euler angles can also be computed by converting from other 3D orientations. Here are a few examples:

rotation matrix > Euler angles

Given a 3D rotation matrix defined as:

$$ \textbf{R} = \begin{bmatrix} R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33} \end{bmatrix}$$

the GlobalZXZ Euler angles ($\alpha, \beta, \gamma$) can be computed as: $$\alpha = arctan(\frac{R_{31}}{R_{32}})$$ $$\beta = arccos(R_{33})$$ $$\gamma = -arctan(\frac{R_{13}}{R_{23}})$$

note that $\beta$ should be within [0,$\pi$]. See other rotation matrix to Euler angle conversions here.

quaternion > Euler angles

Given a quaternion defined as: $$ \textbf{q} = q_0 + q_1\textbf{i} + q_2\textbf{j} + q_3\textbf{k}$$

the GlobalZXZ Euler angles ($\alpha, \beta, \gamma$) can be computed as:

$$\alpha = arctan\left(\frac{q_1 q_3 + q_0 q_2}{-(q_2 q_3 - q_0 q_1)}\right)$$ $$\beta = arccos(q_0^2 - q_1^2 - q_2^2 + q_3^2)$$ $$\gamma = arctan\left(\frac{q_1 q_3 - q_0 q_2}{q_2 q_3 + q_0 q_1}\right)$$

and the BodyZYX Euler angles ($\alpha, \beta, \gamma$) can be computed as:

$$\alpha = arctan\left(\frac{2(q_0 q_1 + q_2 q_3)}{1-2(q_1^2 + q_2^2)}\right)$$ $$\beta = arcsin(2(q_0 q_2 - q_1 q_3))$$ $$\gamma = arctan\left(\frac{2(q_0 q_3 + q_1 q_2)}{1-2(q_2^2 + q_3^2)}\right)$$

Interactive Euler angles

Try it yourself! In the interactive graphic below, drag the rotationX, rotationY, and rotationZ bars left and right. The rotationOrder box defines the sequence of Euler angles, and the frameOfReference box defines whether the angles are rotated about the Body frame axes or about the Global frame axes. Hope this helps give a more intuitive feel for the different sequences of Euler angles.

 
Peter Shull
Previous

Machine Learning: What are the Key Ingredients?
Next

Why You Should Switch to Python from Matlab